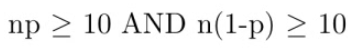Question 1 (a)

The data show a weak but positive association between price and quality rating for these sewing machines. The form of the association does not appear to be linear. Among machines that cost less than $500, there appears to be very little association between price and quality rating. But the machines that cost more than $500 do generally have better quality ratings than those that cost less than $500, which causes the overall association to be positive.

Question 1 (b)

The sewing machine that most affects the appropriateness of using a linear regression model is the one that costs about $2,200 and has a quality rating of about 65. Although the other four sewing machines costing more than $500 generally have higher quality ratings than those costing under $500, their prices and quality ratings follow a trend that suggests that quality ratings may not continue to increase with higher prices, but instead may approach a maximum possible quality rating. The $2,200 sewing machine is the most expensive of all but has a relatively low quality rating, which is consistent with a nonlinear model that approaches a maximum possible quality rating and then perhaps decreases. If a linear model were fit to all of the data, this one machine would substantially pull the regression line toward it, resulting in a poor overall fit of the line to the data.

Question 3 (a)

Household size tended to be larger in 1950 than in 2000. The histograms reveal a much larger proportion of small (1-, 2-, and a-person) households in 2000 than in 1950. Similarly, the histograms reveal a much smaller proportion of large (5-person and larger) households in 2000 than in 1950. Also, the median household sizes can be calculated to be 5 people per household in 1950 compared with 3 or 4 people per household in 2000. The year 1950 displayed slightly in household sizes than the year 2000. Although the interquartile ranges for both years are the same (3 people), the standard deviation (1950: about 2.6 people; 2000: about 2.1 people) and the range (1950: 13 people; 2000: 11 people) are larger for 1950 than for 2000. Both distributions of household size are skewed to the right. In both years, there are a few households with very large families, as large as 14 people in 1950 and 12 people in 2000.

  • Summarizing Distribution (SOCS)

    • Shape

      • Skewed left/right

    • Outlier

      • Q1 - 1.5 * IQR

      • Q3 + 1.5 * IQR

    • Center

      • Mean or Median

    • Spread

      • SD or IQR

Question 3 (b)

The conditions for applying a two-sample t-procedure are: 1. The data come from independent random samples or from random assignment to two groups; 2. The populations are normallv distributed, or both sample sizes are large; 3. The population sizes are at least 10 (or 20) times the sample sizes. The first condition is satisfied because independent random samples were selected for the years 1950 and 2000. The second condition is satisfied because the sample sizes (500 in each group) are quite large, despite the right skewness of the distributions of household sizes in the sample data. The third condition is satisfied because the number of households in the large metropolitan area in both 1950 and 2000 would easily exceed 10 X 500 = 5, 000.

  • Conditions for Sampling Distribution (RIN)

    • Random

      • How the sample is selected

    • Independent

      • N≥10n

      • N: population size

      • n: sample size

    • Normal

      • For

        means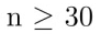

        • C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image168.png

        • If the population is normally distributed, n can < 30

      • For proportions:

        • np 2 10 AND n(l-p) 2 10

Question 4

  • Hypothesis Test

    • Using a Statistic to test a claim about a Parameter

    • Steps (Why Can't Cat Play Instruments)

      • Write the hypothesis

        • Null hypothesis (H0): Parameter = ____

        • Alternative hypothesis (H1/Ha): Parameter > or < or ≠ ______

      • Ckeck conditions (RIN)

        • Random Sample

        • Independent: N >10n

        • Normal:

          • μ: n≥30

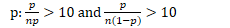
          • C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image384.png

      • Calculate the test statistic

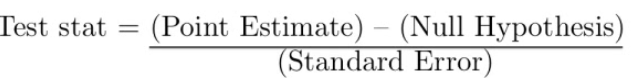
    rest stat (Point Estimate) — (Null Hypothesis) tandar Error

  • Mean

    σ η

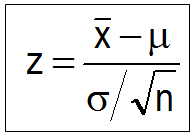
  • Proportion

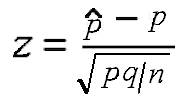
    C:\\6432CA65\\FE01530B-89BD-4F8B-A3E1-55F12080AD12\_files\\image210.png

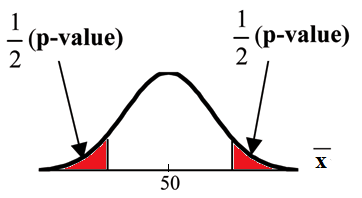
  • Look up the P-value (from Z table)

    • Probability that the null hypothesis (H0) is true, given the sample data you collected

    — (p-value) 2 50 — (p-value) 2

  • Interpret

p < α Reject the null hypothesis do have evidence to support the claim
p > α Fail to reject the null hypothesis do not have evidence to support the claim

  • Step 1

    ![States a correct pair of hypotheses. Let represent the population proportion of adults in the United States who would have answered "yes" about the effectiveness of television commercials in December

    1. Let P08 represent the analogous population proportion in December 2008. The hypotheses to be tested are Ho: = versus Ha • P08 ](./media/image385.png)

  • Step 2

    Identifies a correct test procedure (by name or by formula) and checks appropriate conditions. The appropriate procedure is a two-sample z-test for comparing proportions. Because these are sample surveys, the first condition is that the data were gathered from inde endent random sam le from the two populations. This condition is met because we are told that the subjects were randomly selected in the two different years. Although we are not told whether the samples were selected independently, this is a reasonable assumption given that they are samples of different sizes selected in different years. The second condition is that relative to the proportions involved. This condition is satisfied because all sample counts (622 "yes" in 2007; 1,020 — 622 = 398 "no" in 2007; 676 "yes" in 2008; 1,009 — 676 = 333 "no" in 2008) are all at least 10 (or, are all at least 5). An additional condition may be checked: than 200 million adults in the United States) are much larger than 10 (or, 20) times the sample sizes.

  • Step 3

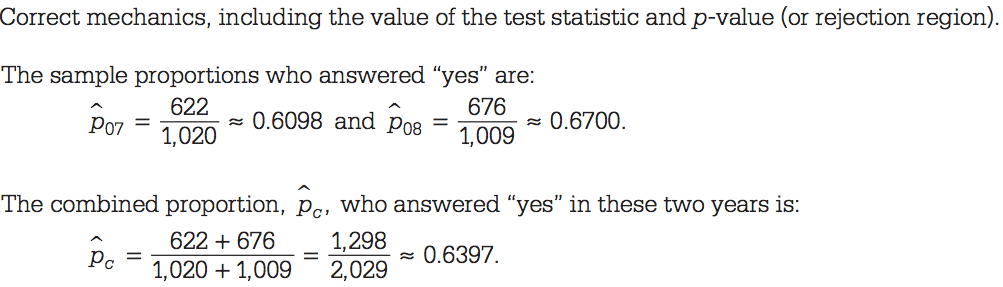
    Correct mechanics, including the value of the test statistic and p-value (or rejection region). The sample proportions who answered "yes" are: 622 0.6098 and P07 676 0.6700. - 1,020 - 1,009 The combined proportion, pc, who answered "yes" in these two years is: 622 + 676 1,298 0.6397. Pc = 1,020 + 1,009 - 2,029

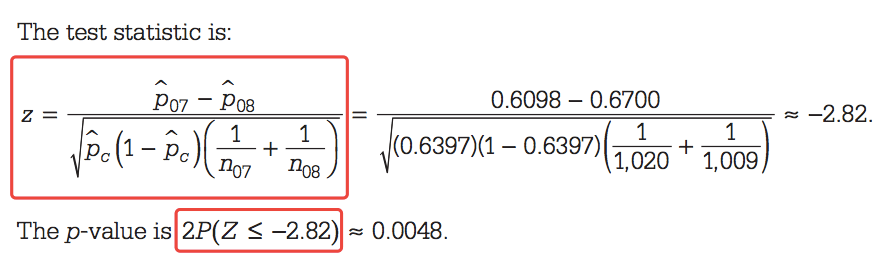
    The test statistic is: P07 - z 1 1107 1108 The p-value is 2P(Z -2.82) 0.6098 - 0.6700 1 - 0.6397) 1, 020 0.0048. -2.82. 1 1, 009

  • Step 4

    State a correct conclusion in the context of the study, using the result of the statistical test. Because this p-value is smaller than any common significance level such as a = 0.05 or a = 0.01 (or, because this p-value is so small), and conclude that the data provide convincing (or, the proportion of all adults in the United States who would answer "yes" to the question about the effectiveness of television from December 2007 to December 2008.

Question 5 (a)

In the context of the=j a Type Il error means ailin to re ect the null h othesis that 35 percent of adult residents in the city are able to pass the test when, realit less than 35 percent are able to pass the test. Th€äääéäuæof this error is that the council would not fund the program, and the city would continue to have a smaller proportion of physically fit residents than the council would like.

  • Type I: falsely think alternative hypothesis is true (1 false), DO reject the null hypothesis (1 word)

  • Type II: falsely think alternative hypothesis is false (2 falses), DO NOT reject the null hypothesis (2 word)

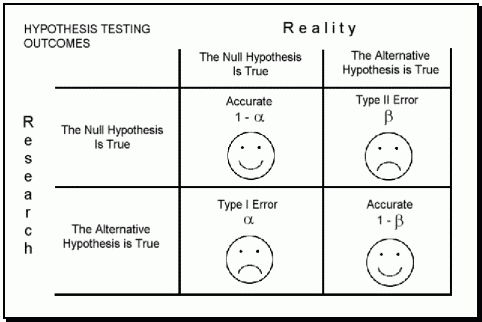
    HYPOTHESIS TESTING OUTCOMES Reality The Null Hypothesis Is True Accurate Type I Error h The Null Hypthesis Is True The Alternative Hypothesis is True The Alternative Hypothesis is True Type Il Error Accurate O

    Type I error (false positive) You're pregnant Type Il error (false negative) You're not pregnant

Question 5 (b)

Because the p-value of 0.97 is larger than a = 0.05, w fail to reject the null hypothesis. There is not convincing evidence that the proportion of adult residents in the city who are able to pass the physical fitness test is less than 0.35. After all, th sam le ro ortion of = 0.416 is actuall hi her than 0.3 which is in of the alternative hypothesis.

Essentially correct (E) if the response correctly completes the following three components: 1. 2. 3. Links the p-value to the conclusion by stating that the p-value is greater than a = 0.05 , OR by stating that OR by correctly interpreting the p-value. Uses context by referring to the(EEEof adult residents who are able to pass the test, OR by referring to the fundin of the program. Makes a correct onclusio that describes the lack of evidence for the alternative hypothesis (Ha : p < 0.35).

Question 5 (c)

This sample because the by recruiting volunteers. It seems reasonable to think that volunteers would be ore h sicall fit than the population of city adults as a whole. Therefore, the sample proportion will population proportion of adult residents in the city who are able to pass the physical fitness test.

Question 6 (a)

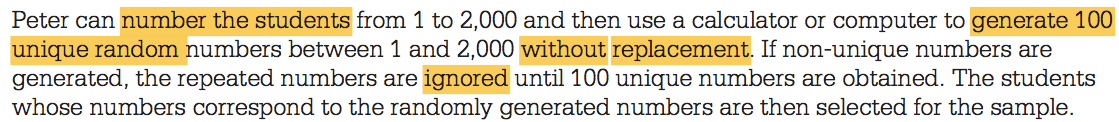
Peter can number the students from 1 to 2,000 and then use a calculator or computer to generate 100 unique random numbers between 1 and 2,000 without replacement. If non-unique numbers are generated, the repeated numbers are ignored until 100 unique numbers are obtained. The students whose numbers correspond to the randomly generated numbers are then selected for the sample.

Question 6 (c)

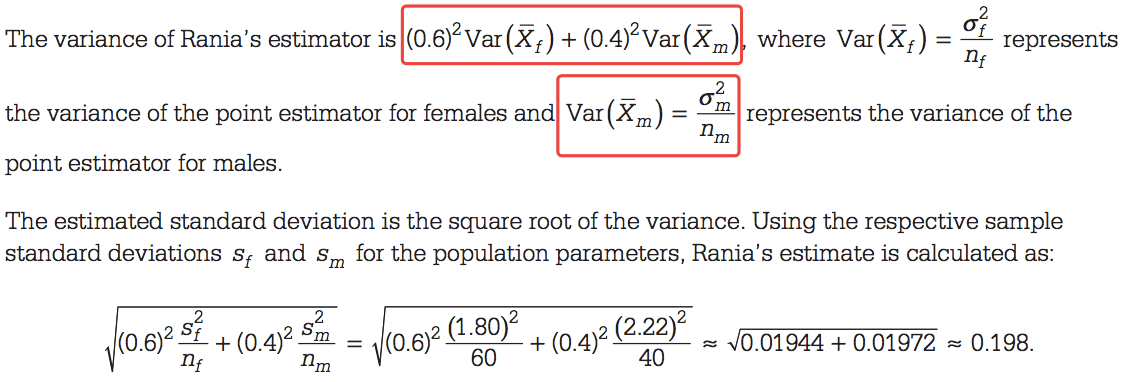
The variance of Rania's estimator is represents rif 2 the variance of the point estimator for females and Var(Rm) — m represents the variance of the n point estimator for males. The estimated standard deviation is the square root of the variance. Using the respective sample standard deviations Sf and sm for the population parameters, Rania's estimate is calculated as: 2 2 (0.6)2 Sf + (0.4)2 sm n 2 (1.80)2 2 (2.22)2 = (0.6) + (0.4) 60 40 0.01944+0.01972 = 0.198.

Question 6 (d)

The comparative dotplots from Rania's data reveal that the distribution of the number of soft drinks for females appears to be quite different from that of males. In particular, the centers of the distributions appear to be significantly different. Additionally, the variability of values around the center within gender in each of Rania's dotplots appears to be considerably less than the variability displayed in the dotplot of Peter's data. Rania's estimator takes advantage of the decreased variability within gender because her data were obtained by sampling the two genders separately. Peter's estimator has more variability because his data were obtained from a simple random sample of all the high school students.

results matching ""

    No results matching ""